Christiaan Huygens nació en La Haya (Holanda) el 14 de abril de 1629 y falleció en La Haya (Holanda) el 8 de julio de 1695. Huygens fue un astrónomo, físico, matemático e inventor neerlandés que desarrolló la teoría ondulatoria de la luz; por ello fue una figura importante de la «Revolución científica».

En física, Huygens hizo grandes contribuciones en óptica y mecánica. Como astrónomo es conocido por el descubrimiento del mayor satélite de Saturno, Titán, en 1655, y por describir la naturaleza de los anillos de Saturno.
Como ingeniero e inventor, Huygens mejoró el diseño de los telescopios e inventó el reloj de péndulo moderno, que hasta la década de 1930 (durante casi 300 años) fue el sistema de cronometraje disponible más preciso.
Como matemático, Huygens tuvo un talento excepcional. Es destacable que fue el primero en idealizar un problema físico mediante un conjunto de parámetros matemáticos. Además, fue el primero en matematizar de forma completa una explicación mecanicista de un fenómeno físico no observable. Por esto se le conoce como uno de los fundadores de la física matemática moderna.
Fueron tantos los campos en los que Huygens sobresalió que su reputación se difundió por toda Europa. Fue elegido socio fundador de la Royal Society de Londres y socio fundador de la Academia de Ciencias de Francia. Había sido invitado por Colbert, ministro de Luis XIV, en 1666.
Nunca se casó ni tuvo hijos, al igual que Newton.
Infancia y formación
Huygens fue el segundo hijo de Constantijn Huygens y Suzanna van Baerle. Este matrimonio tuvo un total de cinco hijos. Su madre falleció con 38 años, tras dar a luz a su última hija; su padre fue un famoso poeta renacentista y secretario de dos príncipes de Orange: Federico Enrique y Guillermo II.
Debido a la alta posición de su padre, Huygens recibió una excelente educación y fue fácilmente introducido en los círculos intelectuales de la época. Hasta los 16 años estudió mecánica y geometría de forma privada. También recibió una gran influencia del matemático francés René Descartes.
En 1645, Huygens se matriculó en derecho y matemáticas en la Universidad de Leiden, donde Frans Van Schooten le impartió clases de matemáticas. En 1647 siguió sus estudios en el Colegio de Orange, en Breda, donde tuvo de profesor a un gran experto en matemáticas, el inglés John Pell.
Frans Van Schooten y Christiaan Huygens se hicieron amigos por su interés en las matemáticas. Tanto es así que años más tarde, en 1657, Huygens contribuyó a la obra de Van Schooten Exercitationum mathematicarum con un artículo sobre la teoría de la probabilidad: «Razonamientos sobre los juegos de azar».
Tras terminar sus estudios en el Colegio de Orange, en 1649, Huygens regresó a casa. Después de considerar brevemente la carrera diplomática, optó por las ciencias y las matemáticas. En la década de 1650 sus habilidades fueron en aumento, algo que no pasaría desapercibido en París.
Correspondencia con Mersenne
El padre de Huygens tenía contacto con el matemático francés Marin Mersenne. Esto propició una correspondencia entre Huygens y Mersenne, en la que Mersenne desafió a Huygens con retos matemáticos. Uno de ellos fue el problema de la catenaria, del que no encontró la solución correcta, pero le permitió descubrir cómo colgar pesos en la cuerda para que cuelgue en forma de parábola.
El primer telescopio de Huygens
A principios de la década de 1650, Huygens y su hermano Constantijn empezaron a pulir lentes para construir telescopios de tipo kepleriano, un modelo diseñado por Johannes Kepler a principios del siglo XVII. Se trata de un tipo de telescopio refractor que usa una lente convexa en vez de una lente cóncava.
Uno de los primeros telescopios de calidad que Huygens construyó fue en 1655 y tenía una distancia focal de unos 337 cm. El ocular que usó era de una sola lente de 79 mm de distancia focal. Como resultado, el telescopio tenía unos 43 aumentos. El telescopio ya no existe actualmente, pero el ocular fue conservado.

Cabe mencionar que Huygens tenía otro objetivo de 722 cm para usar con el mismo ocular. De esta manera, los aumentos podían ser de casi el doble. Se deduce que el ocular era regulable en el tubo. Huygens usó un diafragma justo detrás del objetivo para reducir la apertura y la aberración cromática.
El descubrimiento de Titán
Uno de los primeros objetivos de Huygens al probar su telescopio fue el planeta Saturno. En aquella época, Saturno era uno de los planetas más misteriosos del sistema solar: Galileo Galilei había observado sus anillos sin identificarlos; tenía forma de asa, como unos apéndices laterales.
Con su telescopio, Huygens pudo observar con mayor claridad los anillos de Saturno, y no solo eso, sino que el 25 de marzo de 1655 también observó la presencia de un satélite: Titán, el más grande de Saturno. Después de hacerle un seguimiento durante meses para asegurarse de obtener los datos más precisos acerca de su período y órbita, publicó los resultados en 1656: De Saturni luna observatio nova («Observando la nueva luna de Saturno»).
Titán fue el primer satélite descubierto desde que Galilei había observado en 1610 los cuatro satélites más importantes de Júpiter.
Los anillos de Saturno
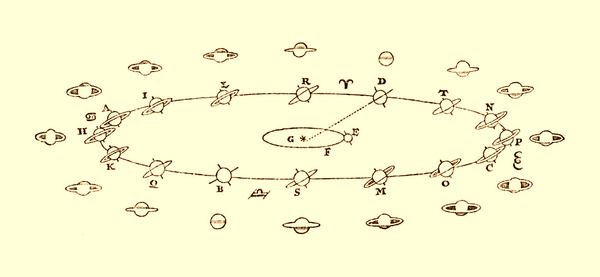
Cuando Huygens empezó las observaciones de Saturno en 1655, el planeta se encontraba en la constelación de los Peces (Pisces). La forma de Saturno era bastante esférica, y los anillos se encontraban más de perfil.
A finales de noviembre de 1655 los anillos estaban totalmente de perfil, por lo que Saturno se veía esférico y con una banda ecuatorial más oscura. A partir de junio de 1656 los anillos volvían a ser visibles. En octubre del mismo año Saturno se volvía a ver de la misma forma que se veía en noviembre del año anterior.
En marzo de 1656, Huygens sugirió que los apéndices o asas de Saturno eran un disco de materia delgado y plano, separado del planeta y situado en su plano ecuatorial. Se dio cuenta de que la apariencia de Saturno “sin anillos” sucedía cuando la Tierra pasaba por el plano ecuatorial del anillo.
La medición del tiempo
Si consideramos la evolución de la tecnología utilizada para medir el tiempo podemos destacar dos períodos. El primer período empieza alrededor del año 1300 en el que se usó un tipo de reloj llamado foliot. Se trataba de un sistema de engranajes y poleas que tenía una precisión de unos 15 minutos diarios.
El reloj de péndulo
Huygens mejoró la tecnología existente inventando el reloj de péndulo en 1656, con una precisión de unos 15 segundos diarios. El reloj de péndulo fue el mecanismo más preciso para medir el tiempo hasta que en 1927 se construyó el primer reloj de cuarzo, en los Laboratorios Telefónicos Bell.
El reloj de péndulo fue idea de Galileo Galilei en el año 1637, y su hijo empezó la construcción en 1649, pero no la finalizó.
También es importante destacar que Huygens desarrolló las matemáticas y la forma mecánica para alcanzar la perfección del isocronismo. Con el fin de corregir la desigualdad del día, en 1662 desarrolló tablas de ecuaciones de tiempo.

En 1673, Huygens resumió su trabajo en la obra Horologium oscillatorium («El reloj de péndulo»). Esta obra es considerada como una de las tres obras más importantes del siglo XVII sobre mecánica, junto con «Dos nuevas ciencias» (1638) de Galilei y «Principios matemáticos de la filosofía natural» (1687) de Isaac Newton.
Matemáticas
La primera publicación sobre matemáticas de Huygens fueron teoremas para calcular las áreas de las hipérboles, elipses y círculos. Expuso los teoremas en 1651 en la obra Theoremata de quadratura hyperboles, ellipsis et circuli («Teoremas sobre la cuadratura de la hipérbola, elipse y círculo»).
Su siguiente publicación fue De circuli magnitudine inventa («Nuevos hallazgos en la medición del círculo»), en 1654. En este tratado, Huygens pudo reducir el hueco entre los polígonos circunscritos e inscritos de un círculo, con respecto a los que detalló Arquímedes en su obra Measurement of a circle.
Huygens estuvo en París durante cinco meses en 1655, donde se interesó por los juegos de azar. Allí conoció el trabajo de Fermat, Pascal y Desargues sobre los juegos de azar. Esto lo condujo a ser de los primeros en estudiar la probabilidad, y publicó sus investigaciones en la obra De ratiociniis in ludo aleae («Razonamientos sobre los juegos de azar») el año 1656.
La colisión elástica
Huygens identificó por primera vez las leyes correctas de la colisión elástica en su obra De motu corporum ex percussione («Sobre el movimiento de los cuerpos por colisión»). Realmente terminó esta obra en 1656, pero no se publicó hasta 1703, después de su muerte. En esta obra estudia la colisión de dos péndulos.
La fuerza centrífuga
La fuerza centrífuga para el movimiento circular uniforme fue uno de los mayores descubrimientos de Huygens. Las lecturas que realizó de Galileo Galilei y René Descartes lo motivaron, pero no hay que olvidar que este trabajo derivó de sus investigaciones acerca del reloj de péndulo cónico.
Huygens había tratado la fuerza centrífuga en su obra Horologium oscillatorium («El reloj de péndulo») de 1673. No obstante, ya lo había redactado en su tratado De vi centrifuga («Sobre la fuerza centrífuga») de 1659; pero esta obra no se publicó hasta 1703, años después de que hubiera fallecido.
La fórmula que Huygens encontró sobre la fuerza centrífuga para el movimiento circular uniforme es la misma que se sigue usando en la actualidad:
\[F=\frac{mv^2}{r}\]El ocular de Huygens
En 1662, Huygens diseñó un nuevo tipo de ocular que en la actualidad lleva su nombre. Se trata de un ocular formado por dos lentes plano-convexas paralelas; el primer ocular compuesto de la historia. Este ocular funcionaba muy bien con los telescopios aéreos y de gran longitud que se utilizaban.
Huygens construyó telescopios con una distancia focal cada vez más larga, hasta los 60 metros. Entonces se detuvo por las dimensiones del tubo. En la década de 1680 intentó una enorme construcción de un telescopio aéreo, sin cámara, pero resultó ser demasiado sensible al viento y no tuvo éxito.

La teoría ondulatoria de la luz
Huygens hizo su contribución más importante en el campo de la óptica elaborando la teoría ondulatoria de la luz, descrita en su obra Traité de la lumière («Tratado de la luz»), en 1690. En esta teoría partió del concepto de que cada punto luminoso de un frente de ondas puede considerarse una nueva fuente de ondas. Este principio es conocido con el nombre de «principio de Huygens».
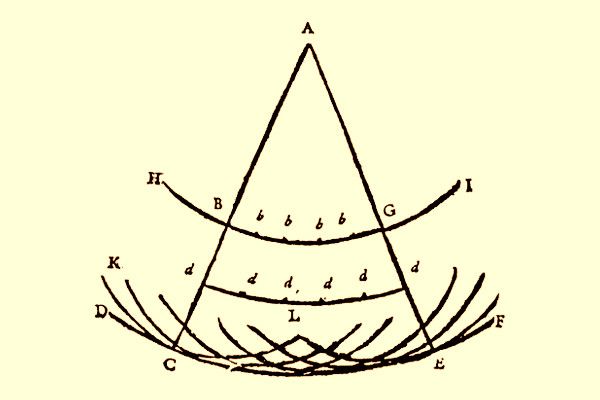
A partir de esta teoría, Huygens explicó varios fenómenos de la luz, como son la reflexión, la refracción y la doble refracción de la luz. A principios del siglo XIX, la teoría ondulatoria de la luz de Huygens quedó totalmente demostrada mediante los experimentos del científico inglés Thomas Young.
La cosmología según Huygens
La última aportación de Huygens hacía referencia a las distancias relativas de las estrellas, todas consideradas como soles del mismo brillo que el nuestro y con planetas que podrían contener vida extraterrestre. Se publicó póstumamente en su obra Cosmotheoros («El observador de las estrellas», 1698).
En esta obra, Huygens defiende el modelo heliocéntrico de Nicolás Copérnico pero con elipses keplerianas. También analiza las dimensiones relativas de los planetas y el Sol. Argumenta que todos los planetas son similares, y que lo que es válido para la Tierra debe serlo para los otros: objetos sólidos con flora y fauna.
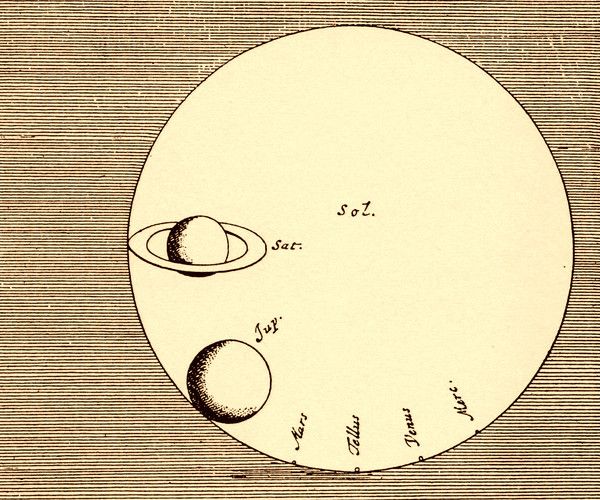
De la misma manera, lo que es válido para nuestro satélite, la Luna, también debe ser válido para los satélites de Júpiter y Saturno. Por ejemplo, si en nuestra Luna hay montañas y valles también debe haberlos en los demás satélites. Pero es probable que no haya ni agua ni aire tanto en nuestra Luna como en las de los planetas exteriores. De hecho, el disco de la Luna se observa nítido, por lo que no debe tener atmósfera, necesaria para la vida.
Es por tanto significativo el hecho en el que Huygens supone la existencia de vida en los planetas y la ausencia de vida en los satélites. Además, sugiere que los habitantes extraterrestres de los otros planetas tienen la misma visión que nosotros de las estrellas fijas, debido a que se encuentran mucho más alejadas.
Cronología resumida de la vida de Huygens
La siguiente tabla muestra de forma resumida los eventos más significativos de la vida de Huygens, ordenados cronológicamente.
| Año | Suceso |
|---|---|
| 1629 | Huygens nace en La Haya el 14 de abril. |
| 1645 | Se matricula en la Universidad de Leiden. |
| 1649 | Termina sus estudios y regresa a casa. |
| 1650 | Empieza a pulir lentes con su hermano Constantijn. |
| 1655 | Descubre el mayor satélite de Saturno: Titán. |
| 1656 | Inventa el reloj de péndulo. Comprende la naturaleza de los anillos de Saturno. Publica «Sobre el movimiento de los cuerpos por colisión». |
| 1659 | Publica «Sobre la fuerza centrífuga». |
| 1662 | Inventa el ocular que lleva su apellido. |
| 1673 | Publica «El reloj de péndulo». |
| 1690 | Publica «Tratado de la luz». |
| 1695 | Huygens fallece en La Haya el 8 de julio. |
Publicaciones de Huygens
- 1650: De iis quae liquido supernatant («Sobre las partes que flotan sobre líquidos»), no publicado.
- 1651: Theoremata de quadratura hyperboles, ellipsis et circuli («Teoremas sobre la cuadratura de la hipérbola, elipse y círculo»).
- 1654: De circuli magnitudine inventa («Nuevos hallazgos en la medición del círculo»).
- 1656: De saturni luna observatio nova («Observando la nueva luna de Saturno»).
- 1656: De ratiociniis in ludo aleae («Razonamientos sobre los juegos de azar»).
- 1656: De motu corporum ex percussione («Sobre el movimiento de los cuerpos por colisión»), publicación póstuma el 1703.
- 1659: De vi centrifuga («Sobre la fuerza centrífuga»), publicación póstuma el 1703.
- 1659: Systema saturnium («El sistema de Saturno»).
- 1673: Horologium oscillatorium («El reloj de péndulo»).
- 1684: Astroscopia compendiaria tubi optici molimine liberata («Telescopios compuestos sin tubo»).
- 1690: Traité de la lumière («Tratado de la luz»).
- 1690: Discours de la cause de la pesanteur («Discurso de la causa de la gravedad»).
- 1698: Cosmotheoros («El observador de las estrellas»).