Una órbita es la trayectoria que realiza un cuerpo celeste alrededor de otro debido a la influencia de su fuerza gravitatoria. Por ejemplo, los planetas, los asteroides y los cometas orbitan alrededor del Sol, pero también los satélites naturales orbitan alrededor de un planeta, como es el caso de la Luna y la Tierra.
En general, la órbita es una trayectoria que se repite de forma regular, sobre todo si es de forma circular o elíptica. Pero no todos los cuerpos celestes repiten su trayectoria: algunos se acercan al Sol y luego se alejan para siempre, pues sus órbitas siguen un trayecto de forma parabólica o hiperbólica.
Introducción histórica
En la historia, las órbitas de los objetos celestes han representado un misterio para los astrónomos. Gracias a la ley de la gravitación universal de Isaac Newton fue posible dar una explicación de los movimientos de los astros.
La necesidad de tener un calendario fiable condujo a una observación sistemática del firmamento, con el consiguiente descubrimiento de que los movimientos de objetos celestes como la Luna y los planetas se caracterizaban por una gran irregularidad. De ahí deriva el concepto de órbita.
El sistema ptolemaico
El modelo planetario que disfrutó de mayor aceptación hasta la época de Galileo fue el sistema ptolemaico. En este sistema, la Tierra figuraba en el centro de toda la creación y estaba rodeada por esferas cristalinas que arrastraban en su movimiento la Luna, el Sol, los planetas y las estrellas.
Esta descripción del mundo permitía describir fácilmente los principales fenómenos que se observaban en el cielo, como el movimiento diario y anual de las estrellas, pero tenía dificultades para explicar las órbitas planetarias, que se pensaba que eran el resultado de la combinación de los diversos movimientos que se sumaban a los de la esfera en que estaba engarzado cada planeta.
Por lo tanto, para poder explicar la complejidad de las órbitas de los planetas, el sistema ptolemaico fue complicándose a su vez.
El sistema ticónico
Una descripción ligeramente diferente y que tuvo escaso éxito se debe al gran astrónomo danés Tycho Brahe, que elaboró un modelo geo-heliocéntrico del universo (llamado sistema ticónico) en cuyo centro también estaba la Tierra, alrededor de la cual solo orbitaban el Sol y la Luna, mientras que los planetas recorrían órbitas alrededor del Sol. Este conjunto, al orbitar alrededor de la Tierra, también arrastraba las estrellas alrededor de ella.
En general, el sistema ticónico respetaba todo lo que podía observarse desde la Tierra, pero era complicado mantenía el geocentrismo ptolemaico.
El sistema copernicano
Gracias a las observaciones de Tycho Brahe, su discípulo Johannes Kepler pudo formular sus famosas leyes que daban fin al geocentrismo, situando el Sol en el centro del universo y relegando la Tierra al papel de un planeta más, dejando solo la Luna orbitando alrededor de nuestro planeta.
Las observaciones con telescopio efectuadas por Galileo aportaron otros argumentos en favor de este modelo. Pero solo gracias a la ley de la gravitación universal de Newton fue posible que esta visión del mundo tuviese una justificación teórica. Así se consolidó la hipótesis de Copérnico (sistema heliocéntrico): el Sol en el centro y los planetas orbitando a su alrededor.
Órbitas cerradas
Las leyes de Kepler establecen que los planetas orbitan alrededor del Sol describiendo órbitas planas y elípticas, en las que nuestra estrella está situada en uno de los focos de la elipse. Estas órbitas son recorridas de manera que la velocidad del planeta es mayor cuanto más cerca está del Sol.
Además, existe una relación muy precisa entre el período de revolución sideral, es decir, el tiempo en el que un planeta tarda en completar una vuelta alrededor del Sol, y la distancia entre el punto orbital del planeta cuando está más alejado del Sol (afelio) y cuando está más próximo (perihelio).
Estas leyes pueden deducirse de la ley de la gravitación universal, que afirma que dos cuerpos se atraen con una fuerza proporcional a sus masas e inversamente proporcional al cuadrado de su distancia. Se trata de la fórmula siguiente:
\[F=G\frac{m_{1}·m_{2}}{r^2}\]Por ejemplo, si la distancia se dobla, la fuerza disminuye cuatro veces; si la distancia se triplica, la fuerza disminuye nueve veces, y así sucesivamente.
Órbitas abiertas
Naturalmente, en la época de Kepler y luego en la de Newton, las órbitas más estudiadas eran las de los planetas, porque se trataba de objetos celestes muy conocidos, y su comportamiento era estudiado desde hacía siglos.
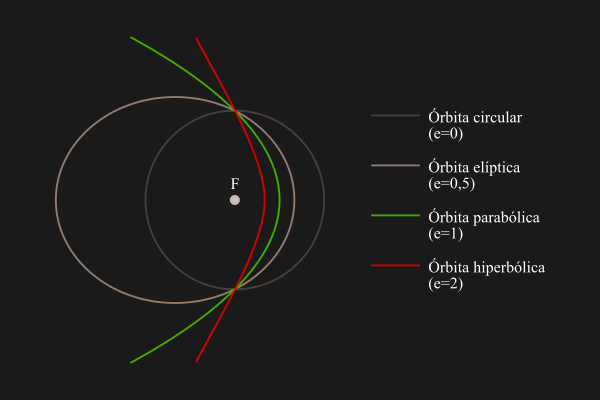
La ley de la gravitación no solo prevé órbitas elípticas, es decir, cerradas, en las que los planetas vuelven periódicamente sobre sus pasos. También puede ocurrir que un objeto provenga de una distancia muy lejana y que, después de pasar cerca del cuerpo que lo atrae, se aleje de él para siempre.
En este caso, el cuerpo atraído recorre una órbita que puede ser de forma parabólica o hiperbólica, en la que el Sol también ocupa uno de los focos, a pesar de ser una órbita abierta. Los objetos típicos que recorren este tipo de órbitas son, en general, algunos cometas y asteroides.
Uno de los éxitos de la gravitación universal fue precisamente el reconocimiento de que los cometas eran objetos del sistema solar, cuyas órbitas podían ser explicadas con la ley de la gravitación. Mientras que en la antigüedad se pensaban que los cometas eran fenómenos atmosféricos.
Además, Edmond Halley descubrió que existía un cometa que reaparecía cada 76 años. Halley supuso que siempre se trataba del mismo objeto y predijo su siguiente aparición. Cuando ésta se realizó con puntualidad, la ley hallada por Newton recibió una confirmación que no admitía réplica.
Al contrario del cometa Halley, muchos otros cometas provienen de las profundidades del espacio sideral y están destinados a marcharse sin volver a aparecer cerca del Sol. Por lo tanto, estos cometas que se mueven en órbitas hiperbólicas no serán vistos de nuevo desde la Tierra.
Parámetros orbitales
¿En qué se diferencian dos órbitas? Naturalmente, una primera diferencia entre dos recorridos orbitales reside en la mayor distancia (afelio) o menor distancia (perihelio) entre el cuerpo orbitante y el cuerpo que lo atrae.
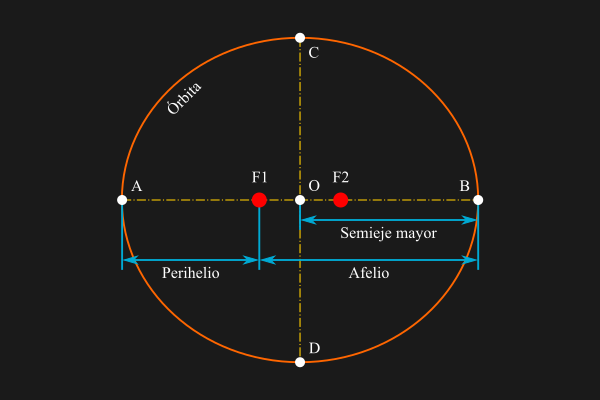
Otro parámetro importante de una órbita es el semieje mayor, que corresponde a la mitad del diámetro más largo. El semieje mayor representa la distancia media de un cuerpo hasta el cuerpo que lo atrae. Esta distancia puede ser probada matemáticamente, y está relacionada con el período orbital sideral.
El período orbital sideral es el tiempo que tarda un cuerpo en completar una vuelta alrededor del cuerpo que lo atrae. Es importante diferenciarlo del período orbital sinódico: el tiempo que tarda un cuerpo en volver a pasar por el mismo punto del cielo respecto al Sol, observándolo desde la Tierra.
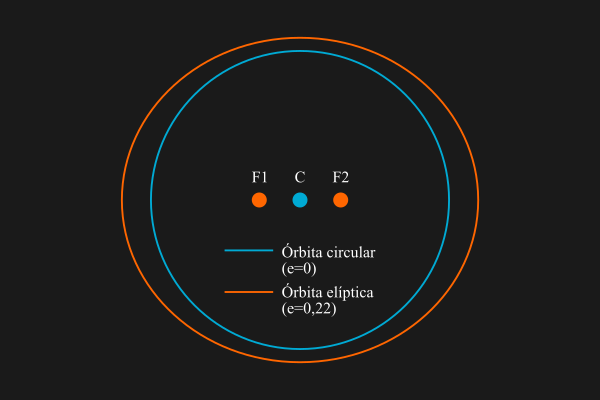
En mecánica celeste, la excentricidad orbital es un parámetro que cuantifica la manera en que una órbita alrededor de otro objeto se desvía de una circunferencia perfecta. Las órbitas elípticas tienen una excentricidad mayor que 0 y menor que 1. En una órbita circular, la excentricidad es 0.
Como es de esperar, el valor de la excentricidad orbital de las órbitas abiertas difiere con el de las órbitas cerradas. Una órbita parabólica tiene una excentricidad equivalente a 1, y una órbita hiperbólica tiene un valor mayor que 1.
La excentricidad orbital (e) se puede calcular dividiendo la semidistancia focal (c) entre el semieje mayor (a). La semidistancia focal es la distancia que hay entre uno de los dos focos de la elipse y el punto del origen. Fórmula:
\[e=\frac{c}{a}\]La inclinación orbital es el ángulo que forma el plano orbital de un cuerpo con respecto a un plano de referencia. En el sistema solar, el plano de referencia es el plano de la órbita de la Tierra, el plano de la eclíptica. La mayoría de astros se mueven en órbitas situadas casi en el mismo plano orbital de la Tierra.
Existen otros cuerpos como los cometas, que se caracterizan por tener órbitas situadas en planos muy inclinados respecto a la eclíptica. Por ejemplo, el planeta enano Plutón tiene la órbita inclinada 17,2°. Más acentuado es el caso del cometa Swift-Tuttle, que da origen a la lluvia meteórica de las Perseidas (lágrimas de San Lorenzo), pues su plano orbital es casi perpendicular a la eclíptica.
El descubrimiento de Neptuno
La importancia de los estudios de las perturbaciones producidas por los planetas sobre los objetos del sistema solar ha sido fundamental para nuestro conocimiento del universo. Gracias al estudio del comportamiento de Saturno y Urano se descubrió la existencia de Neptuno.
Tanto Saturno como Urano presentaban irregularidades en sus órbitas que no podían explicarse del todo con la influencia de los objetos conocidos hasta entonces. El mérito fue de Urban Le Verrier, que supuso que estas irregularidades se debían a la presencia de un octavo planeta hasta entonces no descubierto, lo cual permitió revelar la existencia de Neptuno en el cielo.
John Couch Adams calculó la supuesta posición de Neptuno casi al mismo tiempo que Le Verrier, y de forma totalmente independiente. Mientras que Adams hizo los cálculos desde Cambridge, Le Verrier los hizo desde París.
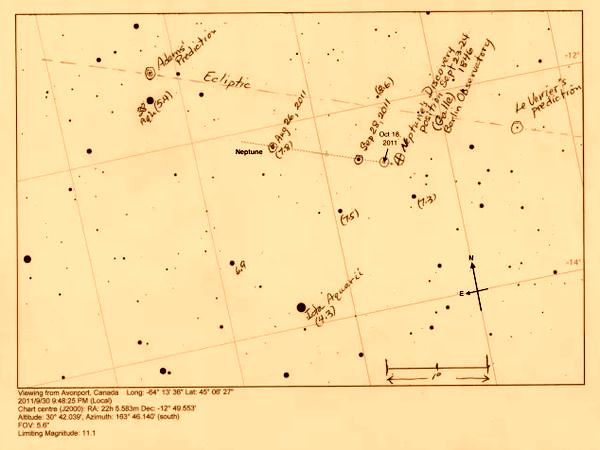
Las previsiones de Adams y Le Verrier fueron confirmadas por muchos observatorios astronómicos pocos días después de la comunicación de sus datos. El descubrimiento de Neptuno significó uno de los resultados más importantes y de mayor éxito de la historia de la mecánica celeste.
El efecto honda
Los cuerpos que más se resienten de las perturbaciones inducidas por los planetas del sistema solar son los cometas, cuyas órbitas son fuertemente alteradas al pasar cerca de los planetas y, en particular, de Júpiter.
El caso más espectacular es el del cometa Shoemaker-Levy, cuya órbita se alteró de tal forma a su paso cerca de Júpiter que lo llevó a colisionar con él. Además, el paso por las proximidades de este objeto produjo la desintegración del cometa debido a las mareas gravitatorias: la diferencia de la fuerza de gravedad entre la parte más próxima a Júpiter y la más alejada.

La alteración de una órbita por el paso cercano a un objeto de gran masa se aprovecha cuando se proyectan los viajes de las sondas interplanetarias. Aprovechando el empuje que se obtiene al pasar cerca de un planeta, estas sondas pueden acelerarse hasta adquirir una velocidad elevada de forma “natural”.
Este efecto, llamado efecto honda, es del todo análogo al que llevó al cometa Shoemaker-Levy a colisionar con Júpiter, con la diferencia de que el cometa sufrió una disminución de velocidad en lugar de una aceleración.
Órbitas de los satélites
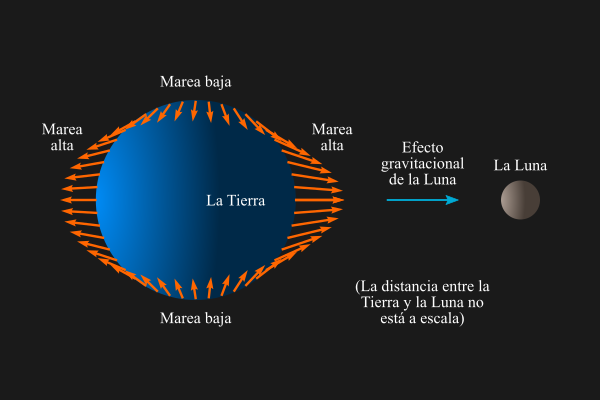
Las órbitas de los satélites naturales se ven alteradas por otros factores, además de la acción gravitatoria del Sol, como es el caso del efecto de la fuerza de marea. La fuerza de marea es un efecto secundario de la fuerza de gravedad, y provoca la existencia de las mareas.
Estos fenómenos se deben a la diferencia entre la fuerza de atracción que el planeta ejerce sobre la parte del satélite más próxima a él y la más alejada. El efecto de marea es el que han sincronizado el movimiento de rotación lunar con el orbital, haciendo que la Luna nos muestre siempre la misma cara.
La Luna tiene una masa lo suficientemente grande y está lo suficientemente cerca de nosotros como para elevar mareas. Este hecho altera la forma del cuerpo grande sin cambiar su volumen: el agua de los océanos se abulta en los dos extremos de un eje que pasa por los centros de gravedad de la Tierra y la Luna. La fuerza de marea tenderá a convertir una forma esférica en una elipsoide.
Sin embargo, su acción no se limita a esto, porque también la Tierra está sincronizando lentamente su movimiento de rotación con el movimiento orbital lunar, alargando la duración del día. Este proceso es lentísimo y tiene una consecuencia adicional: la Luna tiende a alejarse de la Tierra.
Momento angular
Existe una magnitud física llamada momento angular que está ligada al estado de rotación de un sistema físico aislado. En una primera aproximación, éste es el caso del sistema Tierra-Luna. La definición del momento angular viene dada por el producto del momento de inercia por la velocidad de rotación.
En nuestro caso, el momento angular viene dado por la suma de los momentos angulares terrestre y lunar debidos a los movimientos de rotación y de revolución alrededor del centro de masas. Si uno de ellos se reduce, como está sucediendo con los de rotación de la Tierra y de la Luna alrededor de los respectivos ejes, los otros deben aumentar, cosa que sucede porque está aumentando el movimiento angular asociado a los movimientos orbitales.
La confirmación de la relatividad general
Según las leyes de Kepler, todos los planetas recorren órbitas elípticas, con el Sol situado en uno de los focos. Sin embargo, como hemos visto, la forma de una órbita planetaria puede variar debido a la atracción ejercida por los otros planetas. Así, las elipses descritas por los planetas no son perfectas y, si bien son curvas cerradas, se modifican aunque sea de manera imperceptible.
Existe un caso en el que la alteración de la órbita es suficientemente importante para poder ser detectada en la escala de tiempo de algunos años: la órbita de Mercurio. El movimiento de Mercurio puede definirse con suficiente aproximación como una elipse que gira lentamente en el plano orbital.
Este comportamiento ha representado durante decenios un enigma en el entorno de los astrónomos y de los especialistas en mecánica celeste y astrofísica. El cálculo de las perturbaciones debidas a los otros planetas solo podía justificar, en una mínima parte, el comportamiento de la órbita mercuriana.
Solo con la revisión de la teoría de la gravitación universal realizada por Einstein con su teoría de la relatividad general, se pudo explicar de manera satisfactoria el extraño comportamiento de este planeta. La relatividad general permitía explicar de manera muy precisa la órbita de Mercurio.

Además, cuando Einstein elaboró su teoría, desconocía el problema de Mercurio y solo posteriormente se pensó en calcular las órbitas planetarias utilizando su teoría. Así se halló que la teoría preveía un movimiento de precesión de la elipse descrita por un planeta que estuviese suficientemente próximo al Sol.