Tales de Mileto nació en la ciudad de Mileto (antigua ciudad de Grecia que hoy es Turquía) el año 624 a. de C., y falleció en la misma ciudad el año 546 a. de C.; vivió hasta los 78 años. Tales fue un filósofo, matemático y astrónomo griego que fundó la escuela jónica de filosofía o «escuela de Mileto». Se le considera el «primer filósofo de Occidente» y es uno de los «Siete Sabios de Grecia».
De hecho, Tales era considerado «el más sabio» de los «Siete Sabios de Grecia». Cuando se le preguntó qué era difícil, respondió: “conocerse a uno mismo”; y cuando se le preguntó qué era fácil, respondió que “lo fácil es dar consejos”.
Debido a la falta de documentación histórica se desconoce la fecha exacta de su nacimiento y muerte; el año es lo único que se sabe.

Los grandes aportes de Tales abarcan varias ramas científicas, como la astronomía, la óptica, la física (dinámica y estática) y matemáticas: geometría y álgebra lineal. Tales tuvo un discípulo que terminaría haciendo historia en matemáticas: el gran Pitágoras, conocido por su teorema.
La fama de Tales como astrónomo se basa en la predicción de un eclipse solar. Para algunos historiadores, este logro marcó el comienzo de la ciencia astronómica occidental. Aristóteles lo consideró el fundador de la filosofía jónica, a la que pertenecieron también Anaximandro y Anaxímenes.
Tales rompió con el uso tradicional de la metodología para explicar la naturaleza, lo que fue una gran contribución al pensamiento. Apostó por realizar hipótesis y teorías naturalistas (logos). Al igual que la mayoría de filósofos presocráticos, explicó que el agua es el «arjé»: el principio originario de la naturaleza.
En matemáticas, Tales usó la geometría para calcular la altura de las pirámides y la distancia desde la costa hasta los barcos en alta mar. Es la primera persona conocida en utilizar el razonamiento deductivo aplicado a la geometría, y la primera a la que se le atribuye un descubrimiento matemático.
Tales fue el primer matemático en demostrar que un círculo es bisecado por su diámetro, que el ángulo de un semicírculo es un ángulo recto y que los ángulos en la base de un triángulo isósceles son iguales.
Formación y profesión
Los padres de Tales fueron Euxamias y Cleobulinas, ambos originarios de Fenicia. Debido al hecho de que los jonios comerciaban en Egipto y Babilonia, es muy probable que Tales hubiera visitado Egipto, donde habría recibido enseñanzas en geometría, astronomía y meteorología.

Tales también obtuvo conocimientos científicos en Babilonia. Se sabe desde 2005 que la predicción del eclipse solar del año 585 a. de C. fue gracias al conocimiento de un ciclo de eclipses babilónico. El eclipse ocurrió en medio de una batalla, lo que llevó a detener la guerra y realizar un acuerdo de paz.
Hay una anécdota que cuenta que Tales en una ocasión compró todas las prensas de aceitunas de Mileto después de predecir mediante la meteorología que habría una buena cosecha. Llegado el momento, alquiló las prensas a toda la población, con lo que acumuló una gran fortuna en poco tiempo.
Con este hecho Tales demostró que los filósofos también pueden ser ricos, pero que están más interesados por el saber que por el dinero.
Astronomía
En astronomía, Tales destacó por la predicción del eclipse solar del año 585 a. de C. El eclipse ocurrió el 28 de mayo en medio de una batalla. Los contendientes quedaron muy sorprendidos y pensaron que se trataba de una señal divina. Por temor de un mal augurio negociaron un acuerdo de paz.
Según Heródoto:
«En las diferentes batallas que se dieron, hubo una nocturna en el año sexto de la guerra que ambas naciones proseguían con igual suceso, porque en medio de la batalla misma se les convirtió el día repentinamente en noche; mutación que Tales de Mileto había predicho a los jonios, fijando el término de ella en aquel año mismo en que sucedió.» (Heródoto I, 74–2)

No obstante, algunos expertos afirman que en la época de Tales no había los conocimientos para hacer esta predicción con rigor científico. Se cree que Tales conoció los «ciclos de saros»: un registro babilónico de eclipses que permitía saber que el fenómeno se repetía cada 223 lunas (18 años y 11 días).
Tales describió la posición de la constelación de la Osa Mayor y pensó que la constelación podría ser útil como guía para los navegantes en alta mar. También calculó la duración del año y las fechas de los equinoccios y los solsticios.
También se le atribuye la primera observación de las Híades, el cúmulo estelar abierto más cercano al sistema solar, y el cálculo de la posición de las Pléyades, otro cúmulo estelar abierto que también es cercano a nosotros.
Matemáticas
En matemáticas, Tales era conocido por su uso de la geometría, tanto en lo teórico como en lo práctico. De hecho, es considerado como la primera persona del mundo occidental que aplicó el razonamiento deductivo a la geometría. Por ende, es considerado el primer matemático occidental.
Sobre la geometría, Tales dijo:
«El más grande es el espacio, porque contiene todas las cosas».
Tales midió la altura de las pirámides de Egipto haciendo uso de sus sombras. Se puso de pie y esperó a que su propia sombra tuviera la misma longitud que su altura. En ese instante midió la longitud de la sombra de las pirámides, ya que por lógica sería también equivalente a su altura.
Tales se propuso medir la altura de las pirámides a cualquier hora del día. Dado que los rayos del Sol son paralelos, plantó un palo en la arena para crear una sombra fácil de medir y obtener la relación entre su altura y su longitud. Después comparó esta proporción con la longitud de la sombra de las pirámides, y así obtuvo su altura. Los dos triángulos formados son triángulos semejantes.
Se establece que dos triángulos son semejantes si tienen los ángulos iguales y sus lados son proporcionales entre sí.
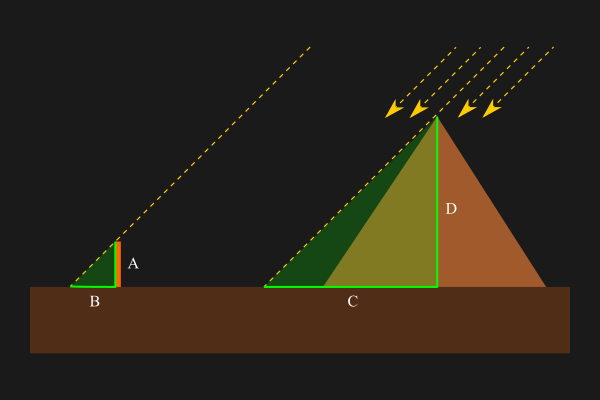
Dado que son triángulos semejantes se cumple lo siguiente:
\[\frac{A}{B}=\frac{D}{C}\]Por lo tanto, se despeja la \(D\) para calcular la altura de la pirámide:
\[D=\frac{A\times C}{B}\]En el caso de la Gran Pirámide de Guiza, Tales midió la longitud de la base de la pirámide (230 m), la longitud de la sombra de la pirámide (65 m), la altura del palo (1,63 m) y finalmente la longitud de la sombra del palo (2 m).
Con estos datos Tales calculó la distancia desde el extremo de la sombra hasta el centro de la pirámide (el segmento \(D\)). Es tan fácil como sumar los 65 m a la mitad de la base de la pirámide (115 m), dando como resultado 180 m.
Conociendo la \(A\), la \(B\) y la \(C\) aplicó los valores a la fórmula:
\[D=\frac{A\times C}{B}=\frac{1.63\,m\times 180\,m}{2\,m}=146.7\,m\]Este método es hoy conocido como el primer teorema de Tales.
El segundo teorema de Tales está enfocado en los triángulos rectángulos, las circunferencias y los ángulos inscritos. Dicho teorema establece que todo ángulo inscrito en una semicircunferencia es un ángulo recto, es decir, de 90°.
Filosofía
Tales de Mileto es considerado el «primer filósofo de Occidente» debido a que intentó explicar de manera racional los fenómenos naturales. Teniendo en cuenta que en su época predominaban las concepciones míticas, es significativo que quisiera encontrar una explicación racional de las cosas.
La explicación universal y racional que sostuvo Tales fue que el agua («arjé») es el origen de todas las cosas que existen.
Cronología resumida de la vida de Tales
La siguiente tabla muestra de forma resumida los eventos más significativos de la vida de Tales, ordenados cronológicamente.
| Año | Suceso |
|---|---|
| 624 a. de C. | Tales nace en Mileto. |
| 585 a. de C. | Predice un eclipse solar. |
| 546 a. de C. | Tales fallece en Mileto. |
Publicaciones de Tales
No se conserva ningún texto suyo y es probable que no dejara ningún escrito para publicación póstuma. Por tanto, no queda constancia escrita de sus aportaciones en los campos de la astronomía, las matemáticas o la filosofía.