Joseph Louis Lagrange nació en Turín (Italia) el 25 de enero de 1736 y falleció en París (Francia) el 10 de abril de 1813; fue francés de origen italiano. Lagrange fue un astrónomo, físico y matemático que hizo grandes contribuciones a la mecánica clásica celeste y a la teoría de números.
Debido a su origen italiano, su nombre inicial fue Giuseppe Luigi Lagrangia.

Lagrange hizo muchas contribuciones significativas a las matemáticas y a la mecánica celeste («puntos de Lagrange»), especialmente a través de su invención del cálculo de variaciones. Una reformulación de la mecánica clásica que Lagrange introdujo se llama «mecánica lagrangiana» en su honor.
Vida y formación
Los padres de Lagrange fueron Giuseppe Francesco Lodovico Lagrangia y Teresa Grosso. Eran italianos y tuvieron once hijos, sin embargo, Joseph Louis fue el único que llegó a la edad adulta. Su padre era militar y tenía una buena posición social, pero perdió muchas propiedades especulando. Estudió en la Universidad de Turín y a los 17 años empezó a mostrar interés en las matemáticas.
Lagrange se sintió atraído por las matemáticas gracias a la lectura de un libro de Edmond Halley sobre análisis matemático.
La vida de Lagrange se puede dividir en tres etapas: desde que nació y hasta el año 1766 vivió en Turín, su ciudad natal. Entonces se trasladó a la ciudad alemana de Berlín para trabajar en la Real Academia Prusiana de las Ciencias, también conocida como Academia de Berlín. El 1787 se trasladó a París (Francia) donde permaneció hasta su muerte, el año 1813.
1. Estada en Turín
La carrera matemática de Lagrange empezó el año 1754 con un artículo presentado al gran matemático alemán Leonhard Paul Euler (1707-1783) en la Academia de Berlín, sobre el cálculo de variaciones. Euler pasó copias de este artículo al matemático francés Pierre Louis Maupertuis (1698-1759).
En este artículo, Lagrange resolvió un tema de debate desde hacía medio siglo, elevándolo hasta la primera línea de los matemáticos de su época.

Fue entonces que Maupertuis ofreció a Lagrange un puesto en la Academia de Berlín, pero se negó. No obstante, sí que fue nombrado miembro extranjero asociado. Además, en 1757 se fundó la Academia de Ciencias de Turín, creada por voluntad del conde Giuseppe Angelo Saluzzo di Monesiglio.
En 1758, desde la Academia de Ciencias de Turín y con ayuda de sus alumnos Lagrange publicó la mayoría de sus primeros escritos, agrupados en cinco volúmenes bajo el título de Miscellanea Taurinensia.
Hay que tener en cuenta que Lagrange dedicó muchas horas al campo de las matemáticas, con un trabajo excesivo que duró varios años. El esfuerzo le afectó seriamente la salud, hasta el punto que los doctores se negaron a ser responsables de su vida a menos que él se tomara en serio la recuperación.
2. Estada en Berlín
El año 1766, Euler abandonó Berlín, por lo que el rey Federico II el Grande de Prusia le pidió a Lagrange que ocupara el puesto de Euler. Textualmente, le dijo que «el rey más grande de Europa debe tener al matemático más grande de Europa». Lagrange aceptó la oferta y ocupó el puesto durante los próximos 20 años.

Durante su estada en Berlín, Lagrange también publicó muchos documentos, entre ellos el trabajo más importante de su vida: Mécanique analytique («Mecánica analítica»). Se publicó en dos volúmenes: el primero el año 1788 y el segundo el 1789. El 1811 publico una segunda edición ampliada del primer volumen.
El 1767, Lagrange se casó con su prima Vittoria Conti, supuestamente influenciado por los amigos que le aconsejaron que el matrimonio era algo necesario para poder ser feliz. Sin embargo, su esposa falleció pronto.
Con el fin de preservar su salud, Lagrange estudió su cuerpo y su mente como si se tratase de una máquina, con el fin de experimentar y calcular la cantidad exacta de trabajo que podía realizar sin perder la salud.
3. Estada en París
Cuando el rey Federico II falleció, el año 1787, Lagrange aceptó la oferta del rey de Francia, Luis XVI, por lo que se trasladó a la capital de Francia: París. Parece ser que el cambio no fue bueno, ya que sufrió un ataque de melancolía y tristeza. Mientras, en el país estaba empezando la revolución francesa.
El 1792, su inexplicable tristeza y su timidez despertaron la compasión de una joven que insistió en casarse con él. Esta chica era Renée-Françoise-Adélaïde Le Monnier de 24 años, y era hija de su amigo Pierre Charles Le Monnier, astrónomo. Él se encariñó cálidamente de ella, por lo que fue un matrimonio feliz.
Mientras duró la revolución francesa, Lagrange estuvo a cargo de una comisión para establecer un nuevo sistema de pesos y medidas. Por su influencia, la comisión acabaría aceptando la subdivisión decimal.
A pesar de que Lagrange había querido salir de Francia, lo cierto es que nunca estuvo en peligro. De hecho, los diferentes gobiernos revolucionarios le otorgaron honores y distinciones. El 1795 ocupó un puesto honorífico en l’École normale, y el 1797 fue nombrado profesor en l’École polytechnique. Junto con Napoleón fue miembro del Senado, y después recibió el título de conde.
El año 1810 Lagrange decidió iniciar una revisión completa de su obra Mécanique analytique («Mecánica analítica»). Pero solo pudo completar una revisión de dos tercios de la obra, ya que el año 1813 falleció.
La obra «Miscellanea Taurinensia»
Una gran parte de los primeros trabajos de Lagrange se encuentra recopilada en los cinco volúmenes que forman la obra Miscellanea Taurinensia.
Del primer volumen se puede destacar, por ejemplo, la teoría de la propagación del sonido o una ecuación diferencial general para el movimiento. De hecho, Lagrange encontró una solución para el movimiento en línea recta. Otros artículos de este tomo tratan las series recursivas, la probabilidad y el cálculo de variaciones.
El segundo volumen contiene un extenso documento con los resultados de varios trabajos del primer volumen, con anotaciones sobre el cálculo de variaciones. El tercero incluye la solución de varios problemas de dinámica por medio del cálculo de variaciones. También contiene artículos sobre el cálculo integral.
Lagrange tardó unos años para empezar a trabajar con los volúmenes cuarto y quinto; fue entre los años 1766 y 1773. Su contribución más importante en estos dos tomos es un tratado en el que explica cómo varias observaciones astronómicas deben combinarse para obtener el resultado más probable.
La mecánica lagrangiana
La reformulación de la mecánica clásica de Isaac Newton es una de las grandes contribuciones de Lagrange al campo de la astronomía, ya que esto simplificó fórmulas y facilitó mucho los cálculos; hoy es conocida como «mecánica lagrangiana». La publicó en la obra «Mecánica analítica» de 1788.
Esta obra expone un gran método analítico general que ahorra trabajo y a través del que cualquier problema en mecánica puede ser expresado en forma de ecuación diferencial. Lagrange intentó reducir la teoría y el arte de solucionar problemas de mecánica a fórmulas generales, con todas las ecuaciones necesarias.
Contribuciones astronómicas
Son muchas las contribuciones que hizo Lagrange a la astronomía. En 1764 publicó un trabajo sobre el movimiento de libración lunar que complementó con una explicación sobre el acoplamiento de marea, con el fin de explicar el motivo por el que la Luna siempre muestra la misma cara a la Tierra.
Dos años más tarde, estando en París, Lagrange publicó un interesante tratado sobre el sistema de satélites de Júpiter. El 1772 publicó un ensayo en el que, intentando resolver el «problema de los tres cuerpos», descubrió los «puntos de Lagrange». En estos puntos se han encontrado asteroides troyanos.
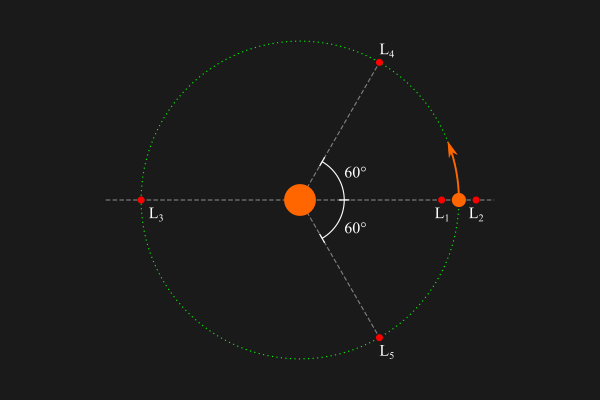
Diagrama que muestra los cinco puntos de Lagrange en un sistema de dos-cuerpos de masa muy diferente (por ejemplo el Sol y la Tierra). En un sistema así, L4–L5 parece que giran en la misma órbita que el cuerpo segundo, aunque de hecho lo hace ligeramente más alejado del primero.
Los puntos de Lagrange son cinco posiciones del espacio respecto a dos cuerpos en las que un tercer cuerpo puede mantenerse respecto a los otros dos sin que la gravedad le afecte. Se simbolizan con L1, L2, L3, L4 y L5.
El 1773 Lagrange publicó un trabajo sobre la gravitación de elipsoides y otro sobre la ecuación secular de la Luna. Este último fue importante porque introdujo la idea de potencial. Expuso que si se conociera el potencial de un cuerpo a un punto externo, se podría encontrar la atracción en cualquier dirección.
El año siguiente Lagrange publicó un tratado sobre el movimiento de los nodos de la órbita de un planeta, y en 1776 publicó otro sobre la estabilidad de las órbitas planetarias. Dos años después, el 1778, redactó un tratado sobre las perturbaciones de los cometas. Le otorgaron varios premios por sus tratados.
Contribuciones matemáticas
Lagrange también hizo grandes contribuciones a las matemáticas. La mayor parte de sus tratados sobre álgebra fueron hechos mientras duró su estada en Berlín. Por ejemplo, el año 1769 publicó la solución entera de las formas cuadráticas.
El 1770 Lagrange publicó un tratado sobre ecuaciones indeterminadas y otro con la teoría de eliminación de parámetros. Un año después publicó un tratado para resolver ecuaciones algebraicas de hasta cuarto grado.
En teoría de números también hizo aportaciones notables. Por ejemplo, demostró el teorema de los cuatro cuadrados: cada entero positivo que no es un cuadrado puede expresarse como la suma de dos, tres o cuatro cuadrados de enteros. Por si fuera poco, Lagrange también logró demostrar el teorema de Wilson.
Las conferencias que Lagrange impartió en l’École polytechnique sobre cálculo diferencial fueron la base de su siguiente obra sobre matemáticas: Théorie des fonctions analytiques, publicada el año 1797 en tres partes. En la primera parte dio una prueba algebraica del teorema de Taylor. En la segunda y tercera trató sobre aplicaciones a la geometría y a la mecánica, respectivamente.
Cronología resumida de la vida de Lagrange
La siguiente tabla muestra de forma resumida los eventos más significativos de la vida de Lagrange, ordenados cronológicamente.
| Año | Suceso |
|---|---|
| 1736 | Lagrange nace en Turín el 25 de enero. |
| 1754 | Presenta un artículo a Euler. |
| 1757 | Funda la Academia de Ciencias de Turín. |
| 1758 | Publica Miscellanea Taurinensia. |
| 1766 | Se traslada a Berlín (Alemania). |
| 1767 | Se casa con Vittoria Conti. |
| 1772 | Descubre los puntos de Lagrange. |
| 1787 | Se traslada a París (Francia). |
| 1788 | Publica «Mecánica analítica». |
| 1792 | Se casa con Renée-Françoise-Adélaïde Le Monnier. |
| 1795 | Ocupa un puesto en l’École normale. |
| 1797 | Es nombrado profesor en l’École polytechnique. Publica Théorie des fonctions analytiques. |
| 1813 | Lagrange fallece en París el 10 de abril. |
Publicaciones de Lagrange
Entre las academias de Turín, Berlín y París, Lagrange llegó a escribir hasta 200 trabajos intelectuales. Algunos de estos solo son tratados, pero todos tienen una extraordinaria calidad. Sus obras más importantes son:
- 1758: Miscellanea Taurinensia.
- 1788: Mécanique analytique («Mecánica analítica»).
- 1797: Théorie des fonctions analytiques.