Eudoxo de Cnido fue un astrónomo, matemático, médico y filósofo griego que planteó el primer modelo planetario basado en un modelo matemático; y se le conoce como «el padre de la astronomía matemática». Nació en Cnido (actual Turquía) el año 390 a. de C. y falleció en la misma ciudad el 338 a. de C.
Los años de su nacimiento y muerte no se conocen con exactitud. Algunas fuentes mencionan el rango de años 408 - 355 a. de C.

La fama de Eudoxo se debe sobre todo a su contribución en astronomía: introdujo las esferas concéntricas e hizo las primeras contribuciones a la comprensión del movimiento planetario. También hizo importantes contribuciones al mundo de las matemáticas. Actualmente, en la Luna y Marte hay cráteres que llevan su nombre, e incluso hay una curva algebraica llamada «campila de Eudoxo».
Formación y profesión
Eudoxo vivió la mayor parte de su vida en la ciudad de Cnido, situada en la costa suroeste de Anatolia, actualmente Turquía. El nombre de «Eudoxo» significa «de buena reputación». Su padre se llamaba Esquines de Cnido, y era un astrónomo aficionado al que le encantaba observar el cielo nocturno.
Como es habitual en muchos filósofos de su época, Eudoxo aprendió mucho en sus viajes. Por ejemplo, en la ciudad italiana de Tarento aprendió las matemáticas de la mano del filósofo y matemático Arquitas. También visitó la isla de Sicilia, donde estudió medicina bajo la tutela de Filisto.
Eudoxo también entró en la Academia de Atenas, una escuela filosófica fundada por Platón, donde estudió filosofía y se interesó por la geometría y las matemáticas. Después estudió astronomía en Heliópolis, una importante ciudad del Antiguo Egipto, donde desarrolló un sistema para predecir los movimientos planetarios basado en esferas concéntricas.
Partiendo de Egipto, Eudoxo viajó hacia el norte. Durante sus viajes reunió un buen grupo de estudiantes y regresó con ellos a Atenas. Según cuentan algunas fuentes, Eudoxo asumió la dirección de la Academia de Atenas y tuvo a Aristóteles como alumno. Finalmente regresó a su ciudad natal, Cnido.

En su regreso a Cnido construyó un observatorio astronómico e impartió conferencias sobre teología, astronomía y meteorología. Se sabe que se casó y tuvo un hijo, Aristágoras, y tres hijas: Actis, Filtis y Delfis.
En Cnido se centró en la teoría de las proporciones y desarrolló su obra más famosa: «Sobre las velocidades», donde presentó su sistema de esferas concéntricas para explicar los movimientos celestiales.
Astronomía
Los astrónomos de la Antigua Grecia intentaron crear modelos planetarios para comprender los movimientos aparentes de los objetos celestes. Eudoxo creó un modelo planetario basándose en modelos matemáticos, razón por la cual se le conoce como «el padre de la astronomía matemática».
De hecho, Eudoxo escribió varias obras sobre astronomía, aunque no perduraron hasta la actualidad. Por ejemplo: «Desapariciones del Sol», seguramente sobre los eclipses, y «Sobre las velocidades», acerca de los movimientos planetarios.
El modelo planetario de Eudoxo propone un universo en el que el Sol, la Luna, los planetas y las estrellas giran alrededor de la Tierra siguiendo círculos perfectos. Se trata de un modelo homocéntrico, con la Tierra en el centro del universo. Esta idea surgió de forma natural, ya que desde la superficie terrestre no llegamos a percibir el movimiento de la Tierra, y en cambio sí que podemos observar el movimiento aparente de los objetos celestes.
Este modelo está compuesto por un sistema de 27 esferas concéntricas rotatorias con un centro común que coincide con el centro de la Tierra. Por eso se llaman «esferas homocéntricas». Estas esferas eran cristalinas y transparentes, y se encontraban concatenadas unas dentro de las otras. Cada una de las esferas se movía sobre sí misma con un eje de rotación diferente.
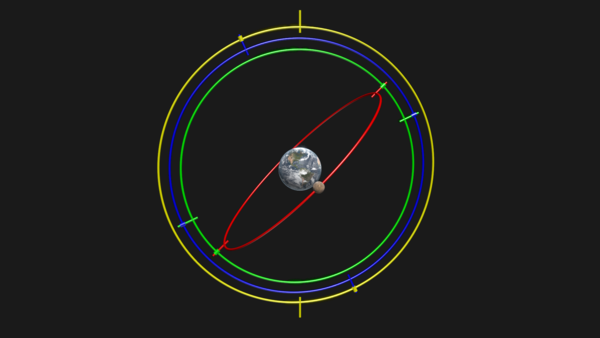
Eudoxo asignó tres esferas para el Sol, tres para la Luna y cuatro para cada uno de los cinco planetas. La última es la esfera de las estrellas fijas. No obstante, nunca trató de explicar la razón del movimiento de estas esferas, ni cómo estaban hechas. Tampoco trató de aproximar las dimensiones de estas esferas.
Gracias a Eudoxo, se pasó del terreno de la especulación filosófica al uso de las matemáticas como herramienta perfecta para describir el sistema solar.
Durante mucho tiempo, la teoría de Eudoxo funcionó para explicar los movimientos aparentes, ya que describía bastante bien el movimiento de los planetas. Cuando las observaciones fueron más precisas, el modelo homocéntrico de Eudoxo perdió la capacidad de explicar la realidad. No obstante, todavía tendrían que pasar muchos años hasta que se abandonaran los modelos geocéntricos.
Matemáticas
Las contribuciones de Eudoxo a la temprana teoría de la proporcionalidad constituyen la base de la explicación general de las proporciones que se encuentra en el Libro V de los «Elementos» de Euclides. De ello se deduce que Eudoxo tuvo una gran amplia comprensión de los números y que sus conocimientos ejercieron una importante influencia sobre Euclides.
De la misma manera, la teoría de Eudoxo sobre las «magnitudes inconmensurables» aparece en el Libro X de Euclides. También es el caso del «método por agotamiento» (o de «exhausción») figura descrita en el Libro XII. Son dos ejemplos más de la influencia de Eudoxo sobre Euclides.
Mediante el «método por agotamiento», Eudoxo demostró que el volumen de una pirámide y el volumen de un cono equivale a un tercio del volumen de un prisma y un cilindro, respectivamente, con la misma base y altura. Seguramente se inspiró en el trabajo de Demócrito sobre la misma materia. Eudoxo también demostró que las áreas de los círculos son proporcionales a los cuadrados de sus diámetros.
El uso del «método por agotamiento» es el precursor del cálculo integral para el cálculo de áreas y volúmenes. Este método fue utilizado de forma magistral por Arquímedes, y no fue superado hasta muchos años después, cuando Newton y Leibniz desarrollaron el cálculo infinitesimal.
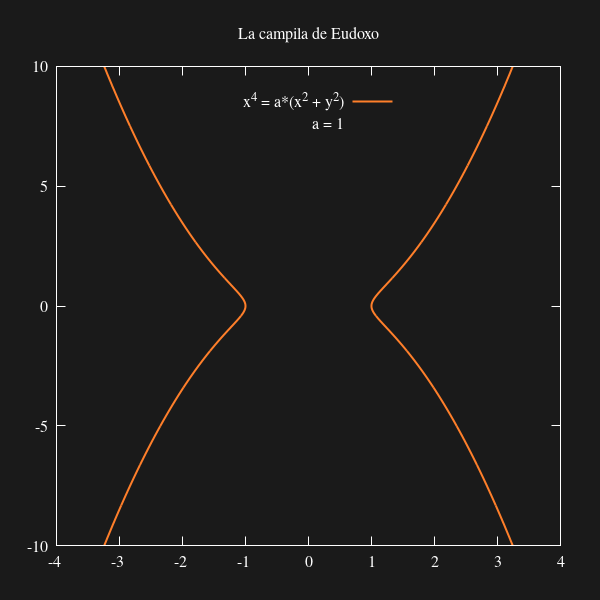
Una curva algebraica lleva su nombre: la «campila de Eudoxo». Eudoxo estudió esta «curva cuártica» en relación con el problema clásico de la duplicación del cubo. Una curva cuártica es una curva plana de cuarto grado.
Ética
En la obra «Ética a Nicómaco», el filósofo griego Aristóteles atribuyó a Eudoxo algunos argumentos a favor del hedonismo. Son los siguientes:
- Todas las cosas, racionales e irracionales, apuntan al placer.
- Las cosas apuntan a lo que creen que es bueno; una buena indicación de lo que es el bien principal sería la cosa a la que apunta la mayoría de las cosas.
- De manera similar, el placer opuesto, el dolor, se evita universalmente, lo que proporciona un apoyo adicional a la idea de que el placer se considera universalmente bueno.
- La gente no busca el placer como un medio para otra cosa, sino como un fin en sí mismo.
- Cualquier otro bien que se pueda imaginar sería mejor si se le añadiera placer, y solo mediante el bien se puede aumentar el bien.
- De todas las cosas que son buenas, la felicidad es peculiar por no ser elogiada, lo que puede mostrar que es el bien supremo.
Cronología resumida de la vida de Eudoxo
La siguiente tabla muestra de forma resumida los eventos más significativos de la vida de Eudoxo, ordenados cronológicamente.
| Año | Suceso |
|---|---|
| 390 a. de C. | Eudoxo nace en Cnido. |
| 367 a. de C. | Viaja a Atenas para estudiar en la Academia. |
| 338 a. de C. | Eudoxo fallece en Cnido. |
Publicaciones de Eudoxo
- Sobre las velocidades
- Desapariciones del Sol
- «Oktaeteris»
- «Phaenomena»
- «Enoptron»